XGBoost是GBDT的改进和重要实现，主要在于：
- 提出稀疏感知(sparsity-aware)算法。
- 加权分位数快速近似学习算法。
- 缓存访问模式，数据压缩和分片上的实现上的改进。
- 加入了Shrinkage和列采样，一定程度上防止过拟合。
提升算法
XGBoost也是一个加法模型，首先其在目标函数中加入了正则化项：
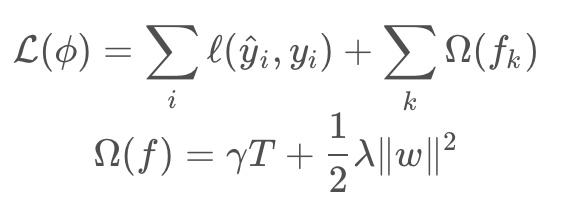
泰勒级数
yi(t)是第i个实例在第t次迭代的预测值，需要加入 ft来最小化以下目标
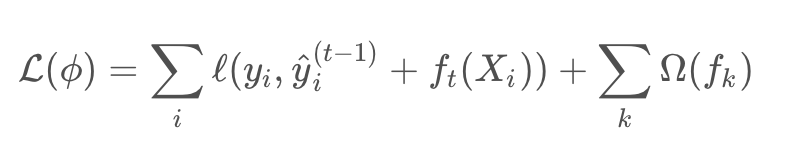
通过泰勒二阶展开近似来快速优化目标函数
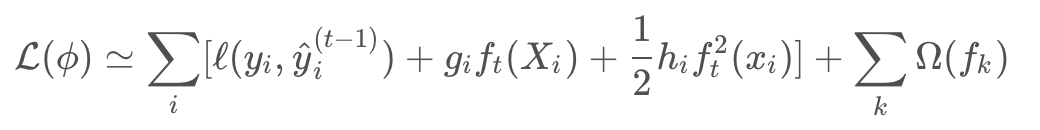
其中
即l的一阶和二阶导数。移除常数项得到：
定义 Ij = {i|q(xi)=j}作为叶子结点j的实例集合。将上式展开为：
计算权重公式：
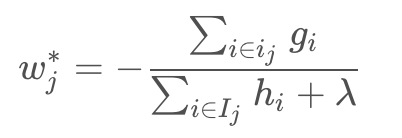
带入目标函数得（一阶和二阶导数合并成了一项）：
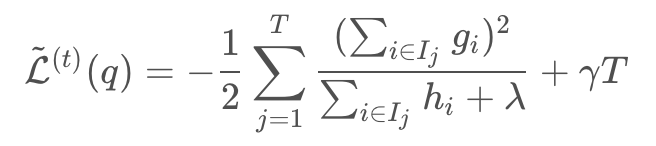
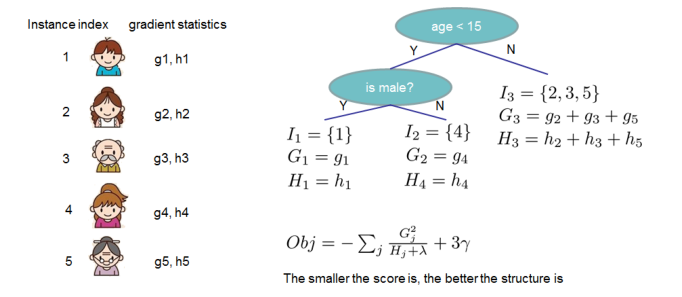
这一项算出的值就是第t棵树要优化目标函数，使其尽量小。下图展示计算过程，目标函数越小越好。
枚举所有可能结构的树是不可能的，通过贪心算法从叶节点开始迭代得添加分支，IL、IR分别是分割点左右分支的实例集，分割的损失下降定义为：
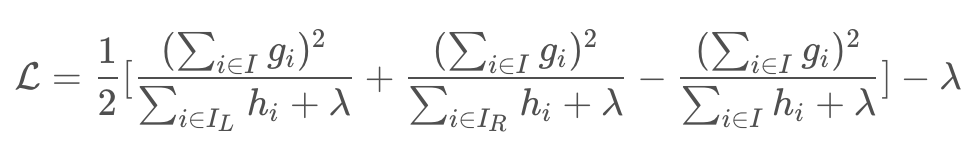
Weighted Quantile Sketch-加权分位
近似算法通过特征百分位点作为划分候选。使集合
代表样本点的第k个特征值和二阶导数。定义排序函数：
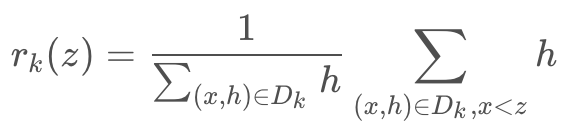
上式表示特征值小于z的样本占整体的比例。目标是找到候选切分点{sk1, sk2, ···,skl}使得：
其中ε是近似因子，这意味着有1/ε个候选点，每个数据点权重是hi,下式说明为什么用它做权重：
其中hi即为平方损失的权重，对于大数据集，找到满足条件的候选分裂是非常重要的。以前的分位算法中没有权重，因为加权数据集没有分位数。
为了解决这个问题，XGBoost提出了新颖的分布式加权的分位数算法，作者理论证明它可以处理加权的数据。总的思路是提出一个支持合并和修剪操作的数据结构，每个操作都被证明保持一定的准确性水平。 证明见。
Sparsity-aware Split Finding
真实数据很多都是稀疏的数据，有很多原因：1.数据中有缺失值。2.统计中频繁出现0条目。3.人工特征工程造成，例如one-hot。为了算法稀疏感知，XGBoost每个树节点加入了默认方向，如图：
当数据值缺失的时候，样本被划分到默认方向，默认方向是通过学习数据获得的，其算法如下图，关键提升在于只看不缺失的实例进入Ik，所提出的算法将不存在作为缺失值处理，并学习处理缺失值的最佳方向。 通过将枚举限制为恒定的解决方案，当不存在对应于用户指定的值时，也可以应用相同的算法。
大多数现有的树学习算法或者只是针对密集数据进行优化，或者需要特定的程序来处理有限的情况，如分类编码。 XGBoost以统一的方式处理所有的稀疏模式。 更重要的是，作者的方法利用稀疏性使计算复杂度与输入中非缺失条目的数量成线性关系。 下图显示了稀疏感知和对Allstate-10K数据集简单实现的比较。 作者发现稀疏感知算法的运行速度比原始版本快50倍。这证实了稀疏感知算法的重要性。
参考